NEU Theory

black ball with a white keyhole shape surrounded by a thick red band representing electron topology

NEU Theory

The Nature of Physical Reality

Menu

Simple Object Topology

Simple Objects

 The Four Primitives of Shape

The basic premise of Simple Object Topology is that all real objects can be described as simple objects by using one or more of the following four primitives of shape:

The rules allow us to deform objects as if they were made of modeling clay. However the initial primitives of shape are conserved unless we perform some topological procedure that allows change.

  • All real objects, first and foremost exist as balls.
  • The ball shape is a primary topological property that can never be removed.

The other three primitives of shape are secondary topological properties that can be added or removed from the primary ball shape by appropriate topological procedures.

  • A ball can have one or more holes. Imagine a donut or a button.
  • A ball can have one or more hollows. Imagine the inside of a tennis ball, or a space station with two or more compartments. A topological shell is a ball with one hollow.
  • A ball with a hollow can have one or more struts. Imagine one or more columns in a room.

That is it. Consider any real object and see how it works. For complex real objects, the description can get very tedious, but you will only need these four primitives of shape.

Topological Translation

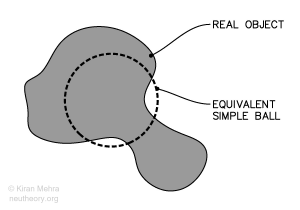An irregular grey shape superimposed with black dotted circle equal in volume to the irregular shape Figure 0.2 – Topological Translation

Topological translation is an imaginative process by which all real objects can be considered as equivalent simple balls by removing deformation. This can visualized by assuming the real object is similar to “modeling clay” which can be reformed into a ball like shape. This reforming is not allowed to remove or add any primitive of shape to the original object, e.g., a cup can be shaped into a donut, or a ball with a handle, as long as the hole remains. No loss of material occurs, and the average density (volume) is maintained. Only the surface area changes. See Figure 0.2.

Topological Operation

A topological operation is an imaginative surgical procedure by which you add, remove, or modify a secondary primitive of shape. This is considered different than topological translation where the primitives of shape before and after translation remain the same.

An topological operation is always clean which means there is no loss of physical quantity after the procedure, though the quantity may take different forms. Making a hole, a hollow, or a strut is a topological procedure.

The following topological procedures are used by the Neu Theory model:

  • openings – example: The spontaneous little bang (beta decay) penetration by the spinning S1 core matter [1a] through the non-spinning S2-S3 membrane matter shell [2a]. This connects the S2-S3 surfaces making a hole with 2 openings in the membrane. The membrane shell becomes a topological ball.
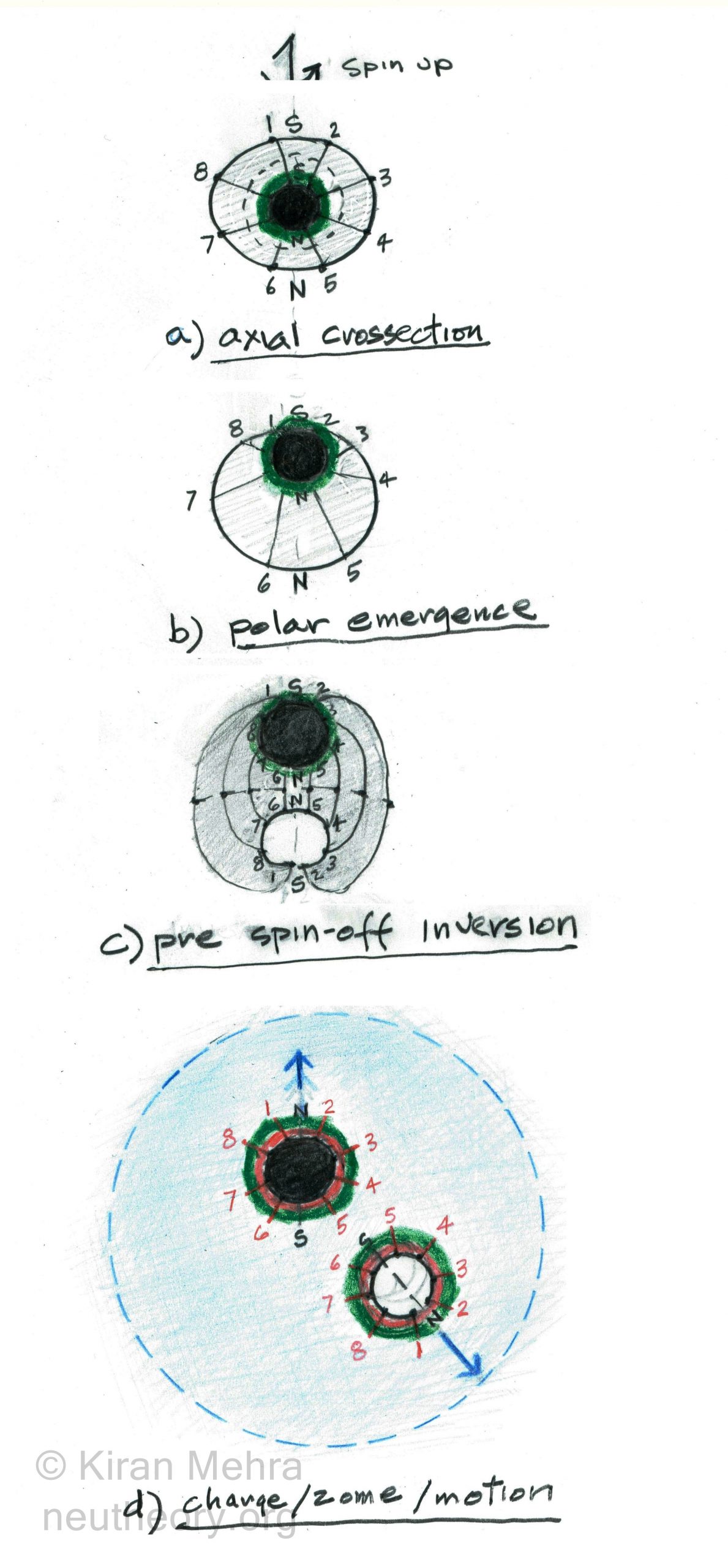  • four drawings showing how the neutron core penetrates through the neutron membrane during the little bang to create electricity, space and motion Figure 3.3 – Neutron Transformation Sequence
  • inversion – example: The spinoff inversion and shrinkage (without loss of volume) by the membrane [2a] matter shell into the detached spinning electron [2b]. The S2 surface changes from a hollow surface into a ball surface. The S3 surface shrinks into a topological void at the center of the electron.
  • shearing – example: The mirror splitting of the delinked absolute spin movement/energy from a plasm matter shell [3a] into the equal and mirror opposite electric dipole charge shells [6+][6-].
  • delinkage – examples: The separation of neucleonic plasm matter [3a] into discrete forms of environmental spin energy as electricity [6+][7+][6-][7-], rise energy as motion [8] and rise energy as space [9]. The delinkage of captive proton core matter [1b] within a nucleus into gamma rays [11] and recoil [8].
  • linkage – example: The synthesis of neucleonic plasm matter [3a] with the synthesis of the deuteron (ab-state).
  • containment – examples: Topologically combined quantum states beneath a neucleonic membrane wall and charge shield as the deuteron (H2) and the helion (He3). The deuteron has one proton core [1b] contained within the plasm [3a] of a neutron cell, for a total of two cores. The helion has two proton cores (1b) contained within the plasm [3a] of a neutron cell, for a total of three cores.
  • fusion – example: The forced clustering of deuterons below a common positive electric charge shield.
  • fission – example: The separation of a large number deuteron charge shield into two or more smaller number deuteron charge shields equal in total number.